Forschende der Leibniz Universität Hannover stellen in einer kürzlich veröffentlichten Studie einen innovativen Ansatz vor, um Ozeangezeitenmodellfehler und nicht modellierte Ozeangezeitenkomponenten in GRACE- und GRACE Follow-On-Distanzmessungen sichtbar zu machen. Dieser Ansatz eröffnet die Perspektive, die Messungen der beiden Missionen für die Entwicklung von Ozeangezeitenmodellen der nächsten Generation zu nutzen.
Igor Koch, Leibniz Universität Hannover
Zeitliche Variationen des Erdschwerefeldes, beispielsweise hervorgerufen durch saisonale Schwankungen des Grundwasserspiegels, den klimabedingten Eismassenverlust oder größere Erdbeben, werden heute mithilfe von Satelliten erfasst. Die zugrundeliegende Idee ist einfach: Da die Bewegung von Satelliten von der Massenverteilung auf der Erde beeinflusst wird, können aus genauen Satellitenpositionsdaten Informationen über die zugrundeliegenden Massen abgeleitet werden. Eine verfeinerte Modifikation dieses Prinzips wird bei den SatellitengravimetrieVerfahren zur Vermessung des Erdschwerefeldes mittels Satelliten. In den vergangenen 20 Jahren wurden verschiedene moderne Varianten realisiert: (1) Laufzeitmessungen zwischen hochfliegenden GPS-Satelliten und einem tieffliegenden Satelliten (high-lo...-Missionen GRACE (2002-2017) und GRACE Follow-On (seit 2018) verwendet. Dabei sind nicht nur die Satellitenpositionen äußerst genau bekannt (dank der GPS-Technologie mit einer Genauigkeit im Zentimeterbereich), sondern auch die Distanz zwischen den Satelliten. Diese kann sogar mit einer Präzision im Mikrometerbereich gemessen werden, was ermöglicht, den Zustand des Erdschwerefeldes mit einer räumlichen Auflösung von wenigen hundert Kilometern und einer zeitlichen Auflösung von etwa einem Monat zu beobachten.
Doch die Bewegung der Satelliten wird nicht nur durch die uns interessierenden Massen auf der Erde beeinflusst, sondern auch durch etliche Störeffekte. Um diese zu eliminieren, müssen sie mithilfe von Modellen aus den gemessenen Distanzdaten herausgerechnet werden. Zu diesen Effekten zählen beispielsweise die Anziehung der Satelliten durch andere Himmelskörper, atmosphärischer Widerstand, aber auch durch Mond und Sonne verursachte Gezeiteneffekte. Insbesondere Massenumverteilungen mit einer kürzeren Periode als die monatliche Auflösung der Erdschwerefeldprodukte müssen präzise modelliert werden. Modellfehler verschlechtern nicht nur die allgemeine Qualität der Schwerefeldprodukte, sondern können dazu führen, dass hochfrequente Störeffekte fälschlicherweise als langsame Massenveränderungen interpretiert werden. Einen solchen herausfordernden Effekt stellen die Ozeangezeiten dar. Um ein genaues Ozeangezeitenmodell zu bekommen, werden numerische Modelle mit Daten von AltimetrieVerfahren zur Höhenmessung von Wasserflächen: Mit Hilfe eines Radars oder Lasers kann vom Satelliten aus beispielsweise die Höhe der Meeresoberfläche oder eines Seespiegels gemessen werden. Hierzu werden kurzwellige Radio- oder Laserimpulse senkr...satelliten kombiniert, welche die Meereshöhe relativ zum Satellitenorbit vermessen. Diese Satelliten decken aber nicht die polaren und subpolaren Gebiete der Erde ab, was zu Modellungenauigkeiten in diesen Regionen führt. Zudem weisen Ozeangezeitenmodelle Schwächen in Küstenregionen auf, wo die Interaktionen der Gezeitenwellen mit den Küstenlinien recht komplex sind, und zudem die Abtastung der Meereshöhe durch die AltimetrieVerfahren zur Höhenmessung von Wasserflächen: Mit Hilfe eines Radars oder Lasers kann vom Satelliten aus beispielsweise die Höhe der Meeresoberfläche oder eines Seespiegels gemessen werden. Hierzu werden kurzwellige Radio- oder Laserimpulse senkr...satelliten zu grob ist.
Mit einem alternativen Ansatz zur Auswertung der GRACE- und GRACE Follow-On-Distanzdaten, welcher im Detail in (Koch et al., 2024) beschrieben ist, gelang es uns, dominante Ozeangezeitenfrequenzen zu identifizieren und die dazugehörigen räumlichen Strukturen herauszuarbeiten. Neben den klassischen Frequenzen, die direkt mit der GravitationGravitation bezeichnet man auch als Schwerkraft oder Massenanziehungskraft. Gravitation ist die Kraft, die zwei oder mehrere Körper aufgrund ihrer Masse aufeinander ausüben. Die bekannteste Gravitationskraft ist die Erdanziehungskraft. Sie bewirkt,... von Mond und Sonne zusammenhängen, lassen sich in den Daten auch weniger erforschte Gezeitenfrequenzen erkennen. Dazu gehören beispielsweise in Küstenregionen auftretende nichtlineare Gezeiten, Effekte aufgrund periodischer atmosphärischer Auflasten und kleinere durch den Mond verursachte asymmetrische Gezeitenkomponenten (Grad-3 Gezeiten), für deren Beobachtung sehr lange Messreihen erforderlich sind. Einige der entdeckten Effekte wurden bislang noch nie in Satellitendaten beobachtet und in der Ozeangezeitenmodellierung vernachlässigt. Die durchgeführte Studie unterstreicht das große Potenzial der GRACE- und GRACE Follow-On-Missionen für die Validierung und Entwicklung neuer Ozeangezeitenmodelle. Dies ist wiederum ein nötiger Schritt, um das aktuelle Fehlerbudget der SatellitengravimetrieVerfahren zur Vermessung des Erdschwerefeldes mittels Satelliten. In den vergangenen 20 Jahren wurden verschiedene moderne Varianten realisiert: (1) Laufzeitmessungen zwischen hochfliegenden GPS-Satelliten und einem tieffliegenden Satelliten (high-lo... zu reduzieren und dadurch ein noch genaueres Verständnis über Massenumverteilungen auf der Erde zu erlangen.
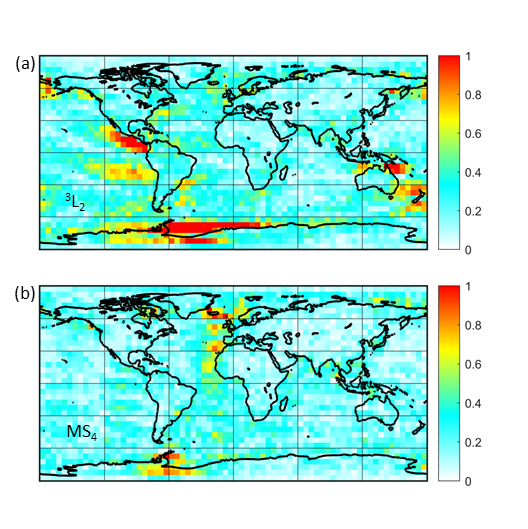
Abbildung 1 zeigt exemplarisch die räumlichen Strukturen der halbtäglichen Grad-3 Gezeit 3L2 und der vierteltäglichen nichtlinearen Gezeit MS4. Um 3L2 von der größeren Grad-2 Komponente L2 zu separieren, sind lange Zeitreihen nötig. MS4 wurde aus den Distanzmessungen mittels eines Modells reduziert, somit stellen die spektralen Amplituden den Fehler des verwendeten Ozeangezeitenmodells dar.
Referenz
- Koch, I., Duwe, M., Flury, J. (2024): Residual and unmodeled ocean tide signal from 20+ years of GRACE and GRACE-FO global gravity field models. Journal of Geophysical Research: Solid Earth, 129, e2024JB029345. doi.org/10.1029/2024JB029345