Satellite-based monitoring of the Earth's gravitational field
The Earth's gravitational field is determined by the mass distribution both inside the Earth and on its surface. It must be measured over long periods of time, i.e. over several decades. Only in this way can we observe climate-relevant processes in the Earth system, such as the melting of ice masses at the poles, the rise in sea level or decreases in groundwater storages anywhere in the world.
As early as in the 1970s, scientists found out that information on changes in the gravitational field could be obtained from the precise measurement of relative differences in the orbits of two identical satellites. However, the measurement principle only works if satellite missions specially developed for this task are placed in an orbit that is as polar and as low as possible.
The orbits of the GRACE satellites
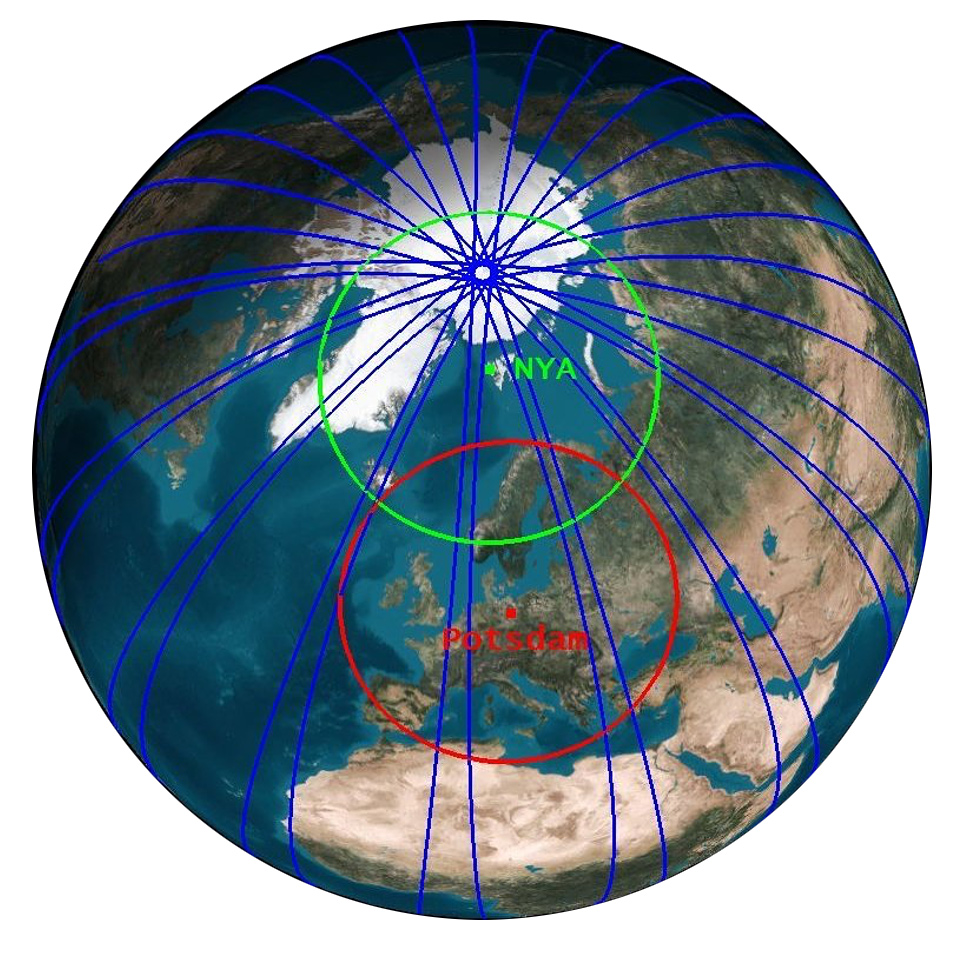
The GRACE and GRACE-FO satellite missions each consist of two identical satellites that fly around the Earth at a distance of about 220 km in the same polar orbit with an initial height of about 490 km. The satellites orbit the Earth in about 95 minutes and thus about 460 times in one month. The repetition times of the associated ground tracks of the satellites (the projection of the orbit onto the rotating surface of the Earth) are not constant in space and time. The polar orbit causes the ground tracks of the orbits to be closer together near the poles than at the equator. This property is exploited by GFZ's satellite receiving station in Ny Ålesund on Spitsbergen, in whose field-of-view the satellites appear during almost every single revolution around the Earth. Since the satellites are not actively kept on prescribed orbits, but move without propulsion under the influence of the Earth's gravitational fieldThe Earth's gravitational field is made up of the Earth's gravitational pull and the latitude-dependent centrifugal acceleration caused by the Earth's rotation. The matter in and on the Earth is not evenly distributed. Water, loose sediments (such as..., the spatial distance from neighboring ground tracks at a given latitude is also not fixed in time. In the case of GRACE-FO, they have so far ranged between 48 km (August 2021) and 146 km (January 2020) over Germany. In rare cases, the satellites fly along the same paths at intervals of a few days (e.g. five days in March/April 2023) on so-called repetitive orbits, so that the spatial distances of these ground tracks are then even greater.
The Instruments
Each satellite is equipped with a GPS (Global Positioning System) receiver for location determination and temporal referencing of the measurement data. In addition, a triaxial accelerometer is located in the centre-of-mass on each spacecraft for direct measurements of non-gravitational forces caused by friction in the residual atmosphere (at the satellites' flight altitude) or the radiation pressure of the sun. Star cameras and additional inertial sensors are used to determine the satellite's orientation in space. The centrepiece is a microwave (K/Ka band) based instrument that continuously measures the distance between the two satellites to within a few thousandths of a millimetre. In addition, a "Laser Ranging Interferometer" (LRI) was installed on GRACE-FO as a technology demonstrator for future gravity field missions, which reduces the measurement noise of the distance measurements by at least a factor of 100 as compared to GRACE. As a further source of information for orbit determination, each satellite also carries a retroreflector for laser-based distance measurements from Earth, which was developed and manufactured at the GFZ. This retroreflector is also regularly targeted by GFZ’s SLR station in Potsdam.
The measuring principle
The highly accurate measurement of the distance or its spatio-temporal variation between the satellites is essential for determining the highly accurate Earth gravity fields, because mass variations primarily cause changes in the orbital velocity of the satellites. The accuracy of the microwave measurement is only a few thousandths of a millimetre. This corresponds to about one tenth of the diameter of a human hair. The high-frequency measurement noise of the LRI is once again significantly smaller at 2 nanometres and also much lower than required in the original specification (60 nm) before launch. It is thus only in the order of magnitude of the thickness of a DNA strand.
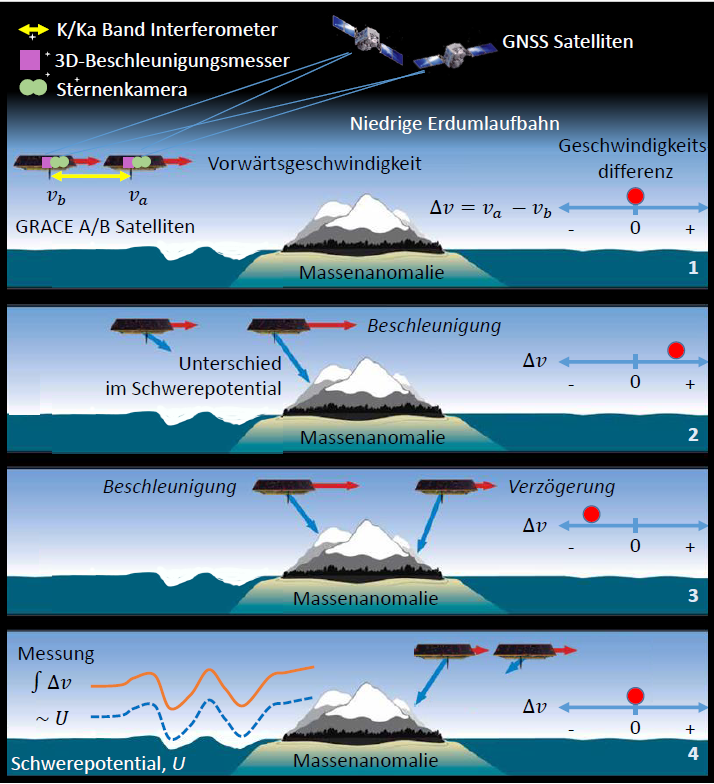
Since both satellites are exposed to identical gravity field anomalies along the same orbit with a slight time delay only (approx. 30 seconds), their relative velocity (Δ v) changes continuously. This leads to small distance changes between the two satellites, which are measured continuously with the microwave instrument or the LRI. Thus, the distance measurements contain information about the slightest differences in the gravity potential U or associated mass anomalies on (e.g., ice masses) and - as a unique selling point of all gravimetric methods - also below the Earth's surface (e.g., groundwater). Usually, these sensor data are collected over 30 days and a mean gravity field model is derived from approx. 460 Earth orbits that is representative for the full month. In a further step, this gravity field model can be displayed as a map of monthly mass anomalies, i.e. mass differences relative to a long-term average.
The figure illustrates the measurement principle schematically. Above an undisturbed ocean surface, the velocity difference of the two satellites vA-vB is zero, since there are no relevant mass anomalies in our example. The length of the (red) velocity vectors is therefore identical (subfigure 1). If the first satellite A flies towards the land surface (subfigure 2), the mass anomaly (here in terms of a mountain) causes an acceleration of satellite A. However, satellite B, which follows 220 km apart, is not (yet) influenced by this additional mass and remains apparently unaccelerated on its orbit. As a result, the velocity difference increases, i.e. the difference of the velocity vectors vA-vB changes from zero to a positive value. In subfigure 3, satellite A moves away from the mass anomaly again, and therefore slows down. Satellite B, on the other hand, is attracted more strongly and increases its velocity, similar to satellite A in subfigure 2. As a result, the velocity difference vA-vB now becomes negative. In subfigure 4, the original state as in sub-figure 1 is resumed again after the trailing satellite has also been slowed down to the original velocity by the mass anomaly just passed, and thus the velocity difference between both satellites over the undisturbed ocean region becomes zero again.
By combining all the sensors mentioned above on a specially designed satellite platform, the GRACE and GRACE-FO missions made it possible for the first time to observe monthly, seasonal and also longer-term mass variations in the Earth’s system. The spatial variations are usually represented in terms of a series expansion in spherical harmonic coefficients (Stokes coefficients) as a function of time and location. GRACE models are typically expanded up to degree 96 (corresponding to a spatial resolution of about 200 km), which requires (n+1)2 = 9401 coefficients. However, due to various limitations of the measurement principle (i.e., polar orbit and associated anisotropy of the distance observations, inaccurate measurements of non-gravitational accelerations, residual errors in the models to correct for sub-monthly mass variations in the ocean, etc.), the coefficients of high degrees and orders are rather poorly determined. Due to the subsequently necessary spatial filtering to suppress these residual errors, some spatial details are therefore lost, so that the resolution limit is effectively about 300 km.
As long as they are based on data from satellite missions alone, gravity maps therefore cannot contain any local details. Satellite gravimetric data must be understood instead as spatial averages. This means that water mass variations with scales smaller than roughly 300 km are averaged out in the data. This also means that spatially clearly defined mass signals (such as lake level variations) are often blurred in the GRACE data. This error influence, also known as "spatial leakage", must be taken into account when interpreting the results. At the same time, it must be kept in mind that satellite gravity field data cannot provide any information about the vertical position of mass anomalies. For the so-called "geophysical signal separation", additional information from numerical models on already well-understood processes such as atmospheric mass redistributions or glacial isostatic adjustment processes in the upper mantle are required. The rigorous identification, quantification and stochastic modelling of those various error influences along the entire processing chain starting from the sensor data (Level-1B) up to the final geophysical mass anomalies (Level-3) are important topics in current research.
Text: Prof. Dr. Frank Flechtner, GFZ
Animation: Measuring principle of the GRACE satellites
Further Reading
- Abich, K., Abramovici, A., Amparan, B., Baatzsch, A., Okihiro, B. B., Barr, D. C., Bize, M. P., Bogan, C., Braxmaier, C., Burke, M. J., Clark, K. C., Dahl, C., Dahl, K., Danzmann, K., Davis, M. A., de Vine, G., Dickson, J. A., Dubovitsky, S., Eckardt, A., Ester, T., Barranco, G. F., Flatscher, R., Flechtner, F., Folkner, W. M., Francis, S., Gilbert, M. S., Gilles, F., Gohlke, M., Grossard, N., Guenther, B., Hager, P., Hauden, J., Heine, F., Heinzel, G., Herding, M., Hinz, M., Howell, J., Katsumura, M., Kaufer, M., Klipstein, W., Koch, A., Kruger, M., Larsen, K., Lebeda, A., Lebeda, A., Leikert, T., Liebe, C. C., Liu, J., Lobmeyer, L., Mahrdt, C., Mangoldt, T., McKenzie, K., Misfeldt, M., Morton, P. R., Müller, V., Murray, A. T., Nguyen, D. J., Nicklaus, K., Pierce, R., Ravich, J. A., Reavis, G., Reiche, J., Sanjuan, J., Schütze, D., Seiter, C., Shaddock, D., Sheard, B., Sileo, M., Spero, R., Spiers, G., Stede, G., Stephens, M., Sutton, A., Trinh, J., Voss, K., Wang, D., Wang, R. T., Ware, B., Wegener, H., Windisch, S., Woodruff, C., Zender, B., Zimmermann, M. (2019): In-Orbit Performance of the GRACE Follow-on Laser Ranging Interferometer. - Physical Review Letters, 123, 031101.
https://doi.org/10.1103/PhysRevLett.123.031101 - Dahle, C., Murböck, M., Flechtner, F., Dobslaw, H., Michalak, G., Neumayer, K., Abrykosov, O., Reinhold, A., König, R., Sulzbach, R., Förste, C. (2019): The GFZ GRACE RL06 Monthly Gravity Field Time Series: Processing Details and Quality Assessment. - Remote Sensing, 11, 18, 2116.
https://doi.org/10.3390/rs11182116 - Flechtner, F., Neumayer, K.-H., Dahle, C., Dobslaw, H., Fagiolini, E., Raimondo, J.-C., Güntner, A. (2016): What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? - Surveys in Geophysics, 37, 2, 453-470.
https://doi.org/10.1007/s10712-015-9338-y - Güntner, A., Gerdener, H., Boergens, E., Kusche, J., Kollet, S., Dobslaw, H., Hartick, C., Sharifi, E., Flechtner, F. (2023): Veränderungen der Wasserspeicherung in Deutschland seit 2002 aus Beobachtungen der Satellitengravimetrie. - Hydrologie und Wasserbewirtschaftung, 67, 2, 74-89.
https://doi.org/10.5675/HyWa_2023.2_1